Kesebangunan Dan Kekongruenan Bangkit Datar Dalam Matematika

Kesebangunan dan Kekongruenan Bangun Datar dalam Matematika - Dalam pelajaran Matematika terdapat bahan pembelajaran mengenai kesebangunan berdiri datar dan kekongruenan berdiri datar. Kesebangunan dan kekongruenan pada berdiri datar sendiri termasuk dalam kategori ilmu Geometri Matematika. Dua buah berdiri datar sanggup dinyatakan sebangun jikalau sisi sisi keduanya mempunyai kesamaan dalam perbandingan nilainya. Kemudian dua buah berdiri datar dinyatakan kongruen jikalau mempunyai persamaan dalam besar sudut dan bentuk ukurannya. Lantas bagaimana konsep kesebangunan segitiga dan kekongruenan segitiga? Bagaimana konsep kesebangunan trapesium dan kekongruenan trapesium?

Dua Buah Bangun Datar Sebangun dan Kongruen

Berdasarkan gambar di atas kita sanggup melihat kesebangunan persegi dan kekongruenan trapesium. Pada dasarnya kesebangunan trapesium, kesebangunan segitiga dan kekongruenan segitiga tidak jauh berbeda dengan prinsip pada gambar di atas. Pada kesempatan kali ini aku akan menjelaskan wacana kesebangunan berdiri datar dan kekongruenan berdiri datar dalam Matematika. Untuk lebih jelasnya sanggup anda simak di bawah ini.

Kesebangunan dan Kekongruenan Bangun Datar dalam Matematika

Dalam pembahasan kesebangunan berdiri datar dan kekongruenan berdiri datar Matematika akan aku bagi menjadi dua sub sajian yakni bahan sebangun dan bahan kongruen. Untuk jenis berdiri datar yang terdapat dalam bahan ini berupa berdiri segitiga dan trapesium. Adapun klarifikasi mengenai kesebangunan segitiga, kekongruenan segitiga, kesebangunan trapesium dan kekongruenan trapesium yaitu sebagai berikut:

Baca juga : Penjelasan Rumus ABC Beserta Pembuktian dan Contoh Soal

Kesebangunan

Hal pertama yang akan aku jelaskan ialah kesebangunan berdiri datar. Lambang kesebangunan sanggup berupa simbol ≈. Dua buah berdiri datar sanggup dinyatakan sebangun jikalau mempunyai ketentuan menyerupai di bawah ini:

• Sudut sudut bersesuaian mempunyai besar yang sama.
• Sisi pada sudut yang bersesuaian mempunyai persamaan dalam perbandingan panjangnya.

Sampai disini apakah anda sudah mengerti bahan kesebangunan berdiri datar? jikalau belum maka simaklah beberapa contohnya. Sebenarnya referensi kesebangunan berdiri datar ataupun kongruen berdiri datar sanggup dengan gampang kita temukan dalam pembelajaran di sekolah.

Kesebangunan Bangun Datar

Gambar Dua Bangun Datar Sebangun

Gambar di atas mengatakan dua buah berdiri datar yang sebangun. Maka dari itu berdiri datar tersebut mempunyai sifat kesebangunan yang ada. Berikut sifat sifat kesebangunan berdiri datar yang terdapat dalam gambar di atas yaitu meliputi:

a. Mempunyai persamaan dalam perbandingan nilai di sepasang sisi yang bersesuaian. Pernyataan ini dibuktikan dengan persamaan di bawah ini:

Sisi PQ dengan TU, maka PQ/TU = 2/4 = ½
Sisi QR dengan UV, maka QR/UV = 2/4 = ½
Sisi RS dengan VW, maka RS/VW = 2/4 = ½
Sisi SP dengan WT, maka SP/WT = 2/4 = ½
Maka dari itu kesimpulannya adalah

b. Mempunyai persamaan pada besar sudut yang bersesuaian. Pernyataan ini dibuktikan dengan persamaan di bawah ini:

∠P = ∠T; ∠Q = ∠U; ∠R = ∠V; ∠S = ∠W

Kesebangunan Segitiga

Gambar Dua Segitiga yang Sebangun

Gambar di atas mengatakan dua buah berdiri segitiga yang sebangun. Maka dari itu berdiri segitiga tersebut mempunyai sifat kesebangunan yang ada. Berikut sifat sifat kesebangunan segitiga yang terdapat dalam gambar di atas yaitu meliputi:

a. Mempunyai persamaan dalam perbandingan nilai di sepasang sisi yang bersesuaian. Pernyataan ini dibuktikan dengan persamaan di bawah ini:

Sisi MN dengan XY, maka MN/XY = 5/10 = ½
Sisi NO dengan YZ, maka NO/YZ = 4/8 = ½
Sisi OM dengan ZX, maka OM/ZX = 3/6 = ½
Maka dari itu kesimpulannya adalah

b. Mempunyai persamaan pada besar sudut yang bersesuaian. Pernyataan ini dibuktikan dengan persamaan di bawah ini:

∠M = ∠X; ∠N = ∠Y; ∠O = ∠Z

Agar anda lebih memahami bahan mengenai kesebangunan berdiri datar dan kesebangunan segitiga di atas. Maka aku akan membagikan referensi gambar dua berdiri datar yang dinyatakan sebangun. Perhatikan gambar di bawah ini!

Gambar Kesebangunan Segitiga

Gambar di atas mempunyai ΔPQR yang sebangun dengan ΔSTR. Maka dari itu diperoleh:

Baca juga : Rumus Integral Tentu dan Tak Tentu Beserta Pengertian dan Contoh Soal

Perhatikan gambar di bawah ini!

Gambar Dua Segitiga Siku Siku yang Sebangun

Jika di buat garis pada segitiga siku siku di atas dari sudut P menuju sisi miring QR. Maka akan memperoleh rumus menyerupai di bawah ini:
PQ² = QS x QR
PR² = RS x RQ
PS² = QS x RS

Kekongruenan

Selanjutnya aku akan menjelaskan wacana kekongruenan berdiri datar. Lambang kekongruenan sanggup berupa simbol ≅. Dua buah berdiri datar sanggup dinyatakan kongruen jikalau mempunyai persamaan ukuran dan bentuk.

Kekongruenan Bangun Datar

Gambar Dua Bangun Datar Kongruen

Gambar di atas mengatakan dua buah berdiri datar yang kongruen. Maka dari itu berdiri datar tersebut mempunyai sifat kekongruenan trapesium. Untuk itu akan diperoleh panjang AB = EF, panjang BC = FG, panjang CD = GH, dan panjang DA = HE. Karena ukuran dan bentuknya yang sama, maka berdiri Trapesium ABCD dengan EFGH dinyatakan kongruen.

Kekongruenan Segitiga
Dua buah segitiga dikatakan kongruen secara geometris jikalau saling menutupi kedua segitiga tersebut dengan tepat. Adapun sifat sifat dalam kekongruenan dua buah segitiga yakni meliputi:

• Memiliki panjang yang sama pada sepasang sisi bersesuaian.
• Memiliki besar yang sama pada sudut bersesuaian.

Selain sifat kekongruenan berdiri datar di atas. Adapula beberapa ketentuan yang menyatakan dua buah segitiga dianggap kongruen yaitu diantaranya:

a. Memiliki besar yang sama pada tiga sisi bersesuaian (sisi, sisi, sisi).

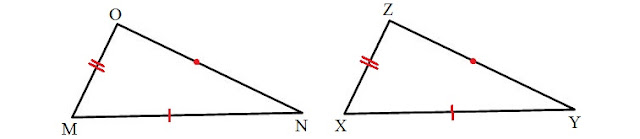Gambar Dua Segitiga Kongruen

Berdasarkan gambar di atas sanggup kita simpulkan bahwa kedua segitiga tersebut kongruen. Maka panjang MN = XY, panjang NO = YZ, dan panjang OM = ZX.

b. Memiliki besar yang sama pada dua sisi dan sudut bersesuaian (sisi, sudut, sisi).

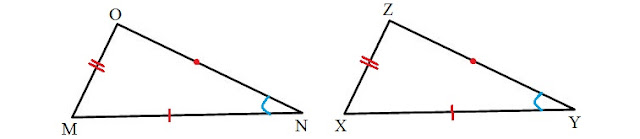Gambar Dua Segitiga Kongruen

Berdasarkan gambar kekongruenan segitiga di atas sanggup kita peroleh kesimpulan bahwa ΔMNO kongruen dengan ΔXYZ. Maka sisi MN = XY, ∠N = ∠Y dan sisi NO = YZ.

c. Memiliki besar yang sama pada dua sudut dan satu sisi apit bersesuaian (sudut, sisi, sudut).

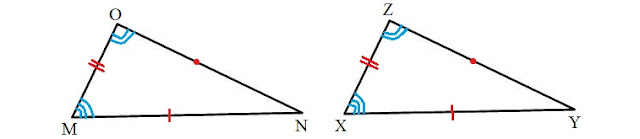Gambar Dua Segitiga Kongruen

Berdasarkan gambar kekongruenan berdiri datar di atas. Kita sanggup memperoleh kesimpulan ΔMNO kongruen dengan ΔXYZ. Maka ∠M = ∠X, sisi MO = XZ, dan ∠O = ∠Z.

Baca juga : Perbandingan Trigonometri Sudut spesial Beserta Contoh Soal

Contoh Soal Kesebangunan dan Kekongruenan

Kita mempelajari bahan kesebangunan dan kekongruenan berdiri datar bukan? Nah, kini saatnya kita menyelam lebih dalam kedalam bahan ini. Dengan mempelajari dan mengerjakan referensi soal kesebangunan dan referensi soal kekongruenan berdiri datar maka kita akan sanggup mengimplementasikan ilmu yang kita dapatkan.

Soal kesebangunan berdiri datar tidaklah terlalu sulit mengingat bahan pembelajaran yang gampang dipahami. Yang diharapkan dalam mengerjakan soal ialah ketelitian dan kesabaran saja. Baiklah, eksklusif saja kita simak beberapa referensi soal kesebangunan dan kekongruenan berdiri datar di bawah.

1. Perhatikan gambar di bawah ini!

Gambar Contoh Soal Kesebangunan Bangun Datar

Gambar persegi panjang ABCD sebangun dengan persegi panjang EFGH. Hitunglah panjang EF, keliling dan luas persegi panjang EFGH?

Pembahasan:
Untuk menghitung panjang EF, maka memakai prinsip kesebangunan berdiri datar menyerupai di bawah ini.

Jawaban Contoh Soal #1

Keliling persegi panjang EFGH = 2 x (EF + EH) = 2 x (6 + 3) = 18 cm
Luas persegi panjang EFGH = EF x EH = 6 x 3 = 18 cm².
Makara panjang EF = 6 cm, keliling persegi panjang EFGH = 18 cm, dan luas persegi panjang EFGH = 18 cm².

2. Perhatikan gambar di bawah ini!

Gambar Contoh Soal Kesebangunan Segitiga

Gambar ΔABC sebangun dengan ΔEFC. Hitunglah panjang BC dan panjang BF?

Pembahasan:
Untuk menghitung panjang BC, maka memakai prinsip kesebangunan berdiri datar menyerupai di bawah ini.

Jawaban Contoh Soal #2

Makara panjang BC dan BF ialah 12 cm dan 4 cm.

3. Perhatikan gambar di bawah ini!

Contoh Soal Kesebangungan pada Bangun Datar

Gambar ΔPQR sebangun dengan ΔSTR. Hitunglah panjang RT?

Pembahasan:
Untuk menghitung panjang RT, maka memakai prinsip kesebangunan berdiri datar menyerupai di bawah ini.

Jawaban Contoh Soal #3

Makara panjang RT ialah 15 cm.

Sekian klarifikasi mengenai kesebangunan berdiri datar dan kekongruenan berdiri datar. Dua berdiri datar dikatakan sebangun jikalau sisi dan sudut yang bersesuaian sama besar. Sedangkan dua berdiri datar dikatakan kongruen jikalau bentuk dan ukurannya sama. Semoga artikel ini sanggup bermanfaat dan terima kasih telah berkunjung di blog ini.

Share this post